I have long wanted to write something about the different binary number representations used in a computer, along their corresponding arithmetic operations. I would have loved to have stumbled upon something like this during my undergraduate years. So, I hope that this will be useful for others who might be looking for a short tutorial-like material on numerical data types used in a computer, in particular integers, fixed-point, and floating-point numbers. In this two part blog-post, I first write about the representation of whole numbers and integers, along with the details of how to add and multiply them.
Whole Numbers
The binary representation of whole numbers is something all of us are familiar with. In the decimal system, the number two hundred and thirty five is represented as the following,
\[235 = 2 \times 10^2 + 3 \times 10^1 + 5 \times 10^0\]In the decimal system, the base is 10 and 10 unique (decimal) digits $0-9$ are used for representing all numbers.
In the binary system, this number has the following representation, where the base is 2 and the digits 0 and 1 are used.
\[\begin{split} 235 =& 1 \times 2^7 + 1 \times 2^6 + 1 \times 2^5 + 0 \times 2^4 + \\ & 1 \times 2^3 + 0 \times 2^2 + 1 \times 2^1 + 1 \times 2^0 \\ =& \left[ 11101011 \right]_2 \end{split}\](Note: \(\left[\cdot\right]_2\) indicates that the number in the square brackets is a binary number. We will use this representation only when there is ambiquity regarding the base of a number.)
A $n$ bit binary number $B$ is written as $B = \left[ b_{n-1}b_{n-2} \ldots b_1b_0 \right]_2$, where $b_i \in [0, 1], \, 0 \leq i \leq n-1$. Let $d(\cdot)$ be the function that coverts a binary number $B$ to its decimal equivalent, \(d(B) = \sum_{i=0}^{n-1} b_i \times 2^i\).
Arithmetic operations on binary numbers are carried out exactly the way we perform decimal arithmetic. We will only consider the addition and multiplication operations here, as the set of whole numbers are not closed under the subtraction and division operations.
Binary Addition can be carried out with the knowledge of the following truth table. Addition of two $n$ bit binary numbers $A$ and $B$ can result in a binary number $C = A + B$ with at most $n+1$ bits.
| A | B | C = A + B | C = A x B |
|---|---|---|---|
| 0 | 0 | 002 | 002 |
| 0 | 1 | 012 | 012 |
| 1 | 0 | 012 | 002 |
| 1 | 1 | 102 | 012 |
Here is an example demonstrating the procedure for adding two binary numbers,
\[\left[ 0110 \right]_2 + \left[ 1101 \right]_2 = \begin{matrix} \begin{array}{r} & 0 & 1 & 1 & 0\\ + & 1 & 1 & 0 & 1\\ \hline 1 & 0 & 0 & 1 & 1 \end{array} \end{matrix} = \left[ 10011 \right]_2\] \[\left[ 6 \right]_{10} + \left[ 13 \right]_{10} = \left[ 19 \right]_{10}\]Binary Multiplication can be carried out with the knowledge of the above truth table. Multipliation of two $n$ bit binary numbers $A$ and $B$ can result in a binary number $C = A \times B$ with at most $2n$ binary bits.
\[\left[ 0110 \right]_2 \times \left[ 1101 \right]_2 = \begin{matrix} \begin{array}{r} & & & 0 & 1 & 1 & 0\\ & & \times & 1 & 1 & 0 & 1\\ \hline & & & 0 & 1 & 1 & 0\\ & & 0 & 0 & 0 & 0 & 0\\ & 0 & 1 & 1 & 0 & 0 & 0\\ 0 & 1 & 1 & 0 & 0 & 0 & 0\\ \hline 1 & 0 & 0 & 1 & 1 & 1 & 0\\ \end{array} \end{matrix} = \left[ 1001110 \right]_2\] \[\left[ 6 \right]_{10} + \left[ 13 \right]_{10} = \left[ 78 \right]_{10}\]Numbers represented using a finite number of bits behave like modulo-$n$ numbers
Numbers represented in computer use a finite number of bits. For example, a 64 bit microprocessor uses 64 bits to represent data, which means that with a single word (64 bits) we can only represent upto a $2^{64}$ different numbers or data types. If we were representing whole numbers then, the maximum number that can be represented is $2^{64} - 1$. Arthimetic operations performed with 64 bit numbers are also restrcited to be 64 bit numbers. This results in these numbers behaving differently under arthimetic operations, compared to numbers with no such restriction on the number of bit. For example, 3-bit numbers under the operation of addition and multiplication will behave like modulo-$2^{3}$ numbers; overflows are ignored and the lower three bits are considered the results of the arthimethic operations.
In general, whole numbers can be represented as discrete, equi-distant points on a number line (infinitely long) as shown in the following figure,
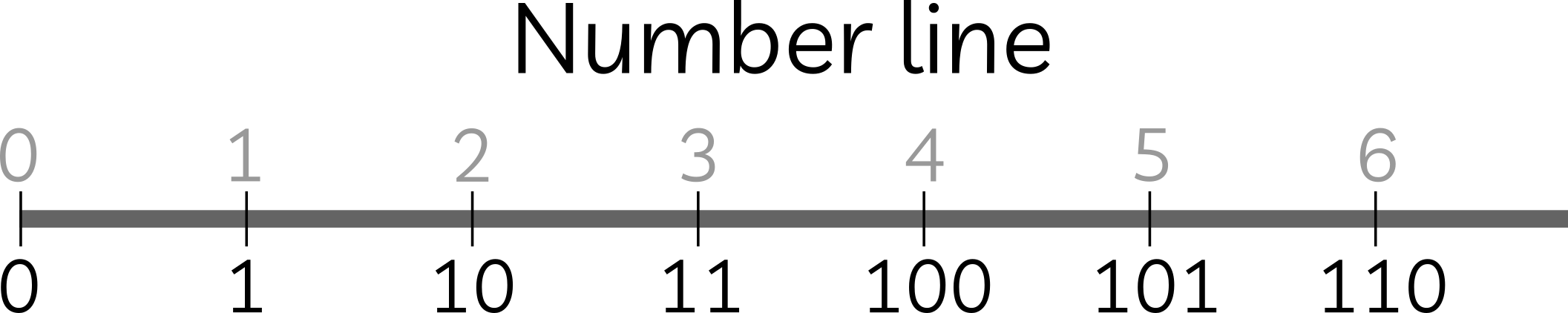
While, the whole numbers represented with a finite number of bits can be represented on a circle (number-wheel) as the following figure,

Integers
When representing negative numbers, on paper, one could simply use the ‘-‘ symbol, e.g. -51 in binary can be written as -110011. Since 0s and 1s are the only available symbols when representing things on a computer, we need a different approach to represent negative numbers: 2’s complement representation. Let’s assume that we working with 3 bit numbers; we can represent upto 8 different numbers. In the 2’s complement representation, the binary representation of positive numbers and zero remain unchanged. However, when we have a negative number $N$, we first take the binary representation of $\vert N \vert$, invert the bits, and add 1 to the inverted numbers.
\[-2 \xrightarrow[\text{binary}]{\text{2 in}} 010 \xrightarrow[\text{bits}]{\text{Invert}} 101 \xrightarrow[\text{1}]{\text{Add}} 110\]In the 2’s complement representation, the most significant bit represents the sign bit, and it is 1 for negative numbers. As the following table indicates.
| Binary No. | Whole number | Integer |
|---|---|---|
| 0002 | 0 | 0 |
| 0012 | 1 | 1 |
| 0102 | 2 | 2 |
| 0112 | 3 | 3 |
| 1002 | 4 | -4 |
| 1012 | 5 | -3 |
| 1102 | 6 | -2 |
| 1112 | 7 | -1 |
We can convert a 2’s complement number to the corresponding decimal number using the following formula,
\[N = -b_{n-1}2^{n-1} + \sum_{i=0}^{n-2} b_i2^i\]The followiing image shows another way to look at 2’s complement numbers.
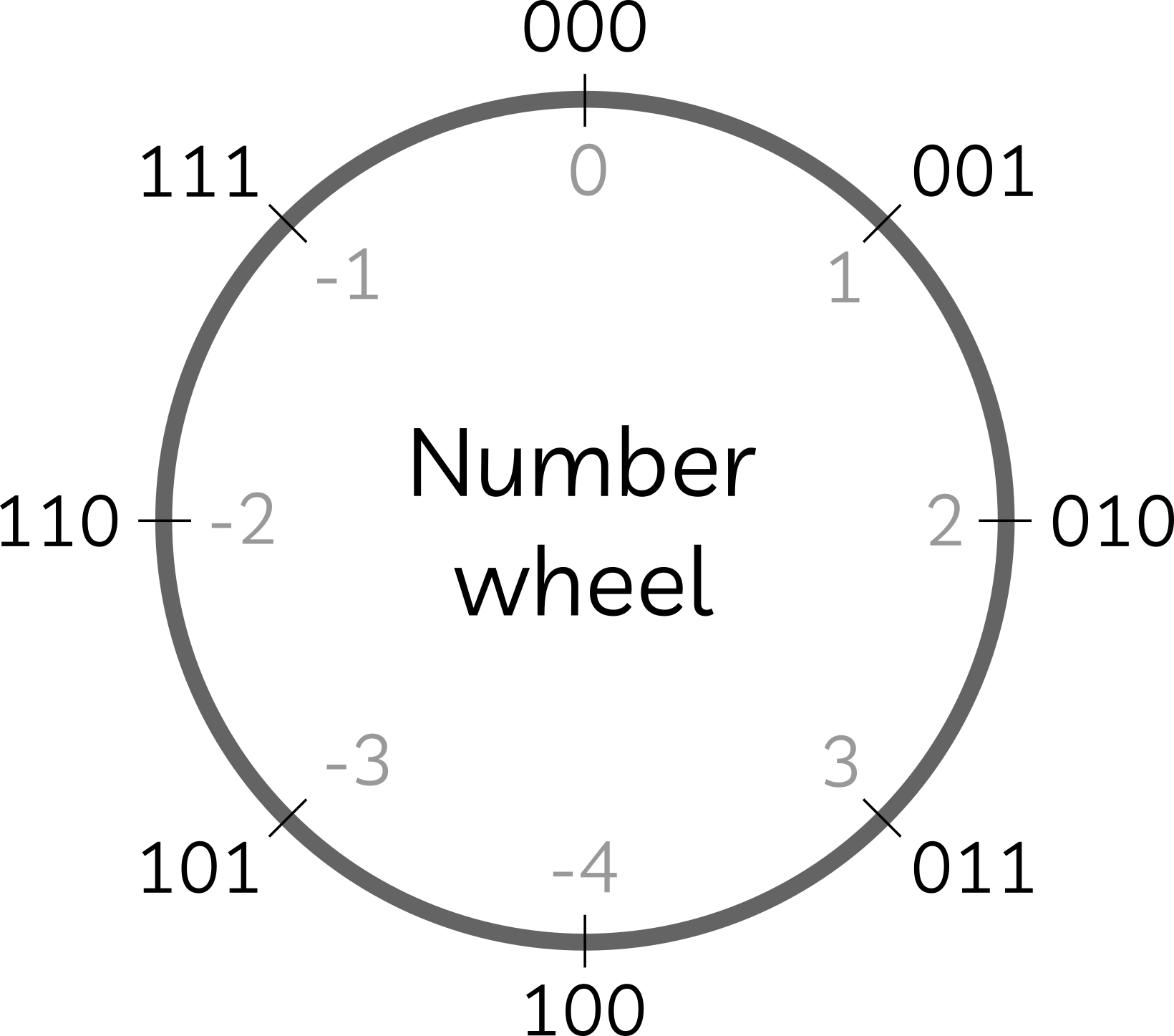
Binary Addition. The truth table for addition remains the same, and we can add two numbers like we did with whole numbers. This handles the addition of both negative and positive numbers, but we need to be careful when interpreting the results because of the sign bit. Addition of numbers corresponds to clockwise movement along the number-wheel, and the 2’s complement representation is such that addition by positive numbers can be seen as clockwise movements, and that of negative numbers as anti-clockwise movement.
However, we need to keep in mind the following conditions, which indicate an overflow:
- Addition of two positive numbers cannot result in a negative number, e.g. \(3 + 2 = [011]_2 + [010]_2 = [101]_2\).
- Addition of two negative numbers cannot result in a positive number, e.g. \(-3 + -4 = [101]_2 + [100]_2 = [001]_2\). Note that the addition of negative numbers in 2’s complement number will result a four bit number. Here we simply ignore the fourth bit.
When adding a positive and negative 2’s complement number, we never run into trouble.
It should be noted that overflow here does not mean the presence of a carryover bit in the \((n+1)^{th}\) position, but rather when the boundary on the number-wheel between extreme positive and negative numbers is crossed by the addition or multiplication operation.
Binary Multiplication. We can multiply 2’s complement numbers like we do with binary whole numbers. The products come out with the appropriate signs provided there is no overflow. Consider wo binary signed numbers $B_1$ and $B_2$. An overflow occurs when: the product $\vert B_1 \times B_2$ is greater than $2^{n-1}$ when the $\text{sign}\left(B_1 \times B_2\right)$ is $-1$, or when the product $\vert B_1 \times B_2$ is greater than $2^{n-1} - 1$ when the $\text{sign}\left(B_1 \times B_2\right)$ is $+1$. There is no overflow when one of the numbers is $0$. You can verify this writing down the product table for 2 bit numbers.
The second part of this blog-post will deal with fixed and floating point numbers.